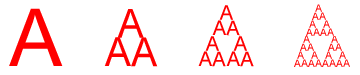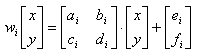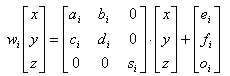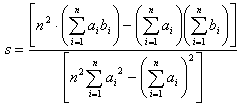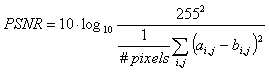FRACTAL IMAGE COMPRESSION

Diese Site wurde kopiert von
http://www.rasip.fer.hr/research/compress/algorithms/adv/fraccomp/index.html
1. Introduction
Ten to fifteen years ago fractal techniques were introduced in computer
graphics. These new ideas came from a mathematical theory called Iterated
Function Systems (IFS). This theory had been developed in 1981 by John
Hutchinson. Michael Barnsley, researcher from Georgia Institute of Technology,
wrote the popular book Fractals Everywhere. The book presents the
mathematics of IFS, a new tool for modeling techniques in computer graphics,
called as the Collage Theorem. The Collage Theorem states what an IFS must be
like in order to represent an image.
This presented an intriguing possibility. If fractal mathematics is good for
generating natural looking images (such as clouds, mountains, ...), could it
not be used to compress images ? Going from a given image to an IFS that can
generate original (more or less), is known as the inverse problem. This
problem remains unsolved. Barnsley, however, thought he had it solved. He
left Institute and found Iterated Systems Incorporated with Alan Sloan. At
January 1988, he announced article in BYTE Magazine about some calculations of
high compression ratio but article did not offer the solution of inverse
problem. At that time nobody knew exactly how to reproduce images at
reasonable compression rates with IFS. The only desperately suggestion to
IFS-based compress given image is so called the Graduate Student Algorithm.
Graduate Student Algorithm:
 | Acquire a graduate student.
 | Give the student a picture.
 | And a room with a graphics workstation.
 | Lock the door.
 | Wait until the student has reverse engineered the picture.
 | Open the door. |
| | | | |
Ironically, it was one of Barnsley's PhD students, Arnaud Jacquin, that
made the Graduate Student Algorithm obsolete. In March 1988, according to
Barnsley, he published a modified scheme for representing images called Partitioned
Iterated Function Systems (PIFS). This broke the ice for a new approach of
research in image encoding.
The idea in Jacquin's method was very simple. An image should not be
considered of as a collage of copies of the entire image, but of copies of
smaller parts of it. For instance, a part of a cloud does not look like an
entire landscape with mountains, sky and clouds, but it probably looks like to
another section of some cloud or some other parts in the image.
Fractal Image Compression was born.
2. What is Fractal Image Compression ?
Consider a special type of photocopying machine that reduces the input image
by a half and reproduces it three times on the copy. What will be happen when
we return back the output of the machine to the input ? Next figure shows the
output images:
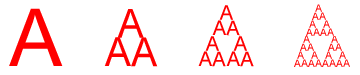
It is obvious that the output images converge to the Sierpinski triangle. This
final image is called attractor for this photocopying machine. Any
initial image (letter 'A' in our case) will be transformed to the attractor if
we repeatedly run the machine. On the other words, the attractor for this
machine is always the same image without regardless of the initial image. This
feature is one of the keys to the fractal image compression.
How can we describe behaviour of the machine ? Transformations of the form as
follows will help us.
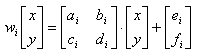
Such transformations are called affine transformations. Affine
transformations are able to skew, stretch, rotate, scale and translate an
input image.
Barnsley suggested that perhaps storing images as collections of
transformations could lead to image compression. His argument went from
possibility to describe the image as a few parameters of affine
transformations. If we have parameters of affine transformations (or
photocopying machine) we can produce the image.
The machine produces self-similarity images called fractals.We need only a few
parameters of affine transformations to produce Sierpinski triangle from any
initial image. But, how to find parameters for any image ? (that is inverse
problem mentioned earlier) Barnsley's dream is to discover algorithm for
calculating these parameters. Unfortunately, images from the nature are very
inapropriate for generating using affine transformations because natural
images are not exactly self-similar. His dream had never came true.
However, the trick exists. But, first of all, lets describe Iterated Function
Systems because Fractal Image Compression is based on it.
Iterated Function Systems
Behaviour of the photocopying machine is described with mathematical model
called an Iterated Function System (IFS). An iterated function system
consists of a collection of contractive affine transformations. This
collection of transformations defines a map 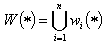
For an input set S, we can compute 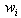 for each i, take the union of these sets, and get a new set W(S).
Hutchinson proved an important fact in Iterated Function Systems: if the
for each i, take the union of these sets, and get a new set W(S).
Hutchinson proved an important fact in Iterated Function Systems: if the 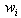 are contractive, then W is contractive. Hutchinson's theorem tells us
that the map W will have a unique fixed point in the space of all
images. That means, whatever image (or set) we start with, we can repeatedly
apply W to it and our initial image will converge to a fixed image.
Thus W completely determine a unique image.
are contractive, then W is contractive. Hutchinson's theorem tells us
that the map W will have a unique fixed point in the space of all
images. That means, whatever image (or set) we start with, we can repeatedly
apply W to it and our initial image will converge to a fixed image.
Thus W completely determine a unique image.
In other words, given an input image (or set) 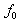 ,
we can repeatedly apply W (or photocopying machine described with W)
and we will get ,
we can repeatedly apply W (or photocopying machine described with W)
and we will get 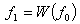 as a first copy,
as a first copy, 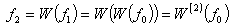 as a second copy and so on. The attractor, unique image, as the result of the
transformations is
as a second copy and so on. The attractor, unique image, as the result of the
transformations is
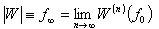
Self-Similarity in Images
Now, we want to find a map W which takes an input image and yields an
output image. If we want to know when W is contractive, we will have to
define a distance between two images. The distance is defined as
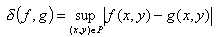
where f and g are value of the level of grey of pixel (for
greyscale image), P is the space of the image, and x and y
are the coordinates of any pixel. This distance defines position (x,y)
where images f and g differ the most.
Natural images are not exactly self similar. Lena image, a typical image of a
face, does not contain the type of self-similarity that can be found in the
Sierpinski triangle. But next image shows that we can find self-similar
portions of the image.
 |
 |
| Original Lena image |
Self-similar portions of the image |
A part of her hat is similar to a portion of the reflection of the hat in the
mirror. Tha main distinction between the kind of self-similarity found in the
Sierpinski triangle and Lena image is that the triangle is formed of copies of
its whole self under appropriate affine transformation while the Lena
image will be formed of copies of properly transformed parts of itself.
These parts are not exact the same; this means that the image we encode as a
set of transformations will not be an identical copy of the original image.
Experimental results suggest that most images such as images of trees, faces,
houses, clouds etc. have similar portions within itself.
Partitioned Iterated Function Systems
For encoding of the image, it is neccesary to divide it into non-overlapped
pieces (so called domains, D) which are each transformed separately. By
partitioning the image into pieces, we must to encode many shapes that are
difficult to encode using an IFS. Because, we have to use Partitioned
Iterated Function Systems (PIFS). PIFS is also based on affine
transformation but, now it describes transformation from one piece of the
image to another (so called ranges, R). Affine transformation mentioned
earlier is able to "geometricaly" transform part of the image but is
not able to transform grey level of the pixel. That is reason, we have to add
a new dimension into affine transformation
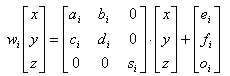
where 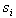 represents the contrast,
represents the contrast, 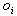 the brightness of the transformation and
the brightness of the transformation and 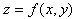 . .
The transformation W has to be contractive in all three directions: x,
y and z. That transformation will be contractive when z
distances are shrunk by factor less than 1 or when each 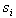 <
1 (some experiments show that 1.2 is still safe). <
1 (some experiments show that 1.2 is still safe).
Now, when we have mathematical "background" we are able to consider
process of encoding images.
Encoding Images
Suppose we have an image f that we want to encode. On the other words,
we want to find a collection of maps 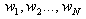 with
with 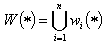 and
and 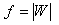 .
That is, we want f to be the fixed point of the map W. The fixed
point is .
That is, we want f to be the fixed point of the map W. The fixed
point is
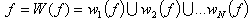
We seek a partition of f into N non-overlapped pieces of the image to
which we apply the transforms 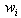 and get back f. This is too optimistic, because the image is not
exactly composed of pieces that can be transformed and fit somewhere else in
the image. What we can expect is another image
and get back f. This is too optimistic, because the image is not
exactly composed of pieces that can be transformed and fit somewhere else in
the image. What we can expect is another image 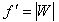 with
with 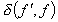 small. On the other words, we seek a transformation W whose fixed point
is not f, but it is close to.
small. On the other words, we seek a transformation W whose fixed point
is not f, but it is close to.
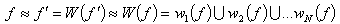
The measure of approximation is distance 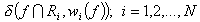
We should find pieces 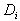 and maps
and maps 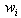 ,
so that when we apply a ,
so that when we apply a 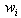 to the part of the image over
to the part of the image over 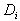 ,
we should get something that is very close to the any other part of the image
over ,
we should get something that is very close to the any other part of the image
over 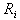 .
Finding the pieces .
Finding the pieces 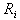 and corresponding
and corresponding 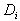 by minimizing distances between them is the goal of the problem.
by minimizing distances between them is the goal of the problem.
At the end, let consider one remarkable example:
Suppose we have to encode 256x256 pixel greyscale image. Let 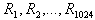 be the 8x8 pixel non-overlapping sub-squares of the image, and let D be
the collection of all overlapping 16x16 pixel sub-squares of the image (general,
domain is 4 times greater than range). The collection D contains
(256-16+1) * (256-16+1) = 58,081 squares. For each
be the 8x8 pixel non-overlapping sub-squares of the image, and let D be
the collection of all overlapping 16x16 pixel sub-squares of the image (general,
domain is 4 times greater than range). The collection D contains
(256-16+1) * (256-16+1) = 58,081 squares. For each 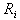 search through all of D to find
search through all of D to find 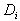 with minimal distances. There are 8 ways (the square can be rotated to 4
orientations or fliped and rotated into further 4 orientations) to map one
square onto another. That means, we have to compare 8 * 58,081 = 464,648
squares with each of the 1024 range squares. Also, a square in D is 4
times smaller as an
with minimal distances. There are 8 ways (the square can be rotated to 4
orientations or fliped and rotated into further 4 orientations) to map one
square onto another. That means, we have to compare 8 * 58,081 = 464,648
squares with each of the 1024 range squares. Also, a square in D is 4
times smaller as an 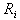 ,
so we have to average a square from D and prepare it for comparing. ,
so we have to average a square from D and prepare it for comparing.
To find most-likely sub-squares we have to minimize distance equation. That
means we must find a good choice for 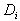 that most looks like the image above
that most looks like the image above 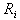 (in any of 8 ways of orientations) and find a good contrast
(in any of 8 ways of orientations) and find a good contrast 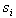 and brightness
and brightness 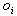 .
For each .
For each 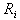 , ,
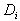 pair we can compute contrast and brightness using least squares regression
which has the least root means square (rms) difference
pair we can compute contrast and brightness using least squares regression
which has the least root means square (rms) difference
. The squared Euclidean distance is used for this purpose 
where 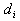 is pixel intensities from
is pixel intensities from 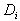 , ,
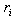 is pixel intensities from
is pixel intensities from 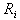 ,
and s and o are contrast and brightness respectively. To compute
contrast and brightness, we have to compute a minimum of the distance. The
minimum of E occurs when the partial derivatives with respect to s
and o are zero ,
and s and o are contrast and brightness respectively. To compute
contrast and brightness, we have to compute a minimum of the distance. The
minimum of E occurs when the partial derivatives with respect to s
and o are zero
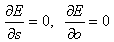 which
occurs when which
occurs when
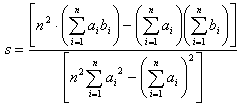 and and

A choice of 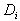 with a corresponding
with a corresponding 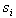 and
and 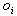 determines a map
determines a map 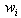 .
Once we have the collection .
Once we have the collection 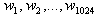 we can decode the image by estimating
we can decode the image by estimating 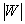 . .
Each transformation requires 8 bits in the x and y direction to
locate the position of 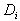 ,
7 bits for ,
7 bits for 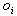 ,
5 bits for ,
5 bits for 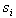 and 3 bits to determine a rotation and flip operation for mapping
and 3 bits to determine a rotation and flip operation for mapping 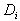 to
to 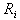 .
We need 31 bits per transformation of 8x8 pixel sub-squares (8x8x8=512 bits),
giving a compression ratio 512/31 = 16.5:1. .
We need 31 bits per transformation of 8x8 pixel sub-squares (8x8x8=512 bits),
giving a compression ratio 512/31 = 16.5:1.
Compression ratio is one of the parameters which determine compression
algorithm. Th second parameter is peak-to-peak signal-to-noise ratio (PSNR).
For 8-bit gray scale images the PSNR is defined as
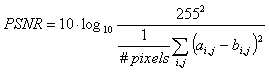 There
are many other modification of mentioned algorithm such as: quadtree
partitioning, HV-partitioning, triangular partitioning, self vector
quantization, convolution transform coding etc. There
are many other modification of mentioned algorithm such as: quadtree
partitioning, HV-partitioning, triangular partitioning, self vector
quantization, convolution transform coding etc.
Encoding Color Images
There is very little work has been published on color fractal image
compression. Recommendation is that not to encode the RGB components
separately but YIQ channels. YIQ channels can be encoded individually; the I
and Q channels should be encode at a lower bit rate than the Y channel.
Other suggestion is to encode the green component of RGB components
individually and try to predict the other (R and B) components.
Fractal Image Compression versus JPEG Compression
At high compression ratios, fractal compression has similar compression and
quality performance as the JPEG standard. Let see some comparisons: 
Original Lena image (184,320 bytes)
 |
 |
JPEG-max. quality (32,072)
comp. ratio: 5.75:1 |
FIF-max. quality (30,368)
comp. ratio: 6.07:1 |
 |
 |
JPEG-med. quality (11,278)
comp. ratio: 16.34:1 |
FIF-med. quality (7,339)
comp. ratio: 25.11:1 |
 |
 |
JPEG-min. quality (8,247)
comp. ratio: 22.35:1 |
FIF-min. quality (3,924)
comp. ratio: 46.97:1 |
These are expected results for Fractal Compression. Some images can be
compressed over 80:1 or higher. We can see worse image quality for higher
compression ratios.
Fractal Compression is an asymmetric process, compression taking a long time
compared with decompression. JPEG/DCT is symmetric process, encoding and
decoding taking the same amount of time. Fractal compression times can be
decreased by using a dedicated hardware. For example, for a 640 x 400 pixel 24
bit colour image, JPEG software compression and decompression took 6 seconds
each, for fractal compression the time was 68 seconds and decompression was
only one second. Reading the original uncompressed image required two seconds.
Another one very important feature of the Fractal Image Compression is Resolution
Independence.
Fractal encoding image has no natural size. It is set of transformations
defined on domains and ranges of the image. When we want to decode image, only
thing we have to do is apply these transformations on any initial image (it is
usually grey rectangle for greyscale images) iteratively. Every iteration is
step closer to the decoded image. After each iteration, details on the decoded
image are sharper and sharper. That means, the decoded image can be decoded at
any size. The extra detail needed for decoding at larger sizes is generated
automatically by the encoding transforms. The next question is: if we decode
an image at larger and larger sizes, will we be able to see atoms of the
Lena's face ? The answer is, of course, no because we are encoding digitized
image which is only approximation of the nature image but on the larger sizes
we do not have "pixelization" effect than we get sharper details.
 |
 |
Lena's eye
original image enlarged to 4 times |
Lena's eye
decoded at 4 times its encoding size |
This feature of Fractal Image Compression is unique.
So why isn't everyone using Fractal Image Compression ?
Fractal Image Compression is still under development. Many different
researchers and companies are trying to develope a new algorithms to reach
shorter encoding time and smaller files. But there are still some problems
with fractal compression. Fractal Compression Standard does not exist ! FIF,
Fractal Image Format is not standardized, is not embedded into any browsers
etc.
In spite of all, total number of publications on fractal image compression is
growing; over 280 papers was published last year.
Show must go on ...
|